“如何評估一個機器學習模型的好壞?”
前情提要
常常在訓練模型時發現在測試資料上可以取得很高的正確率但專案一上線卻發現實際效果不如預期,而為什麼會造成這樣的現象呢?回想以前讀熟時是否常常有個情況是在家寫評量或習題都很順,但實際上真正考試卻不如預期,遭成的原因便是我們只熟記了考古題而非實際題目中的概念或者題目中多了什麼我們沒看過的變化,而機器跟我們一樣往往在測試資料上有很好的表現,只是因為熟記了測試資料中的題目而非真正我們希望機器學到的概念,在機器學習中我們將之稱為過擬合(Overfitting),而閱讀過本篇後希望可以回答以下問題。
- 要如何驗證機器是否有學到該學的東西(Robust)?
- 哪裡學的不好(Explainability)?
- 該往哪裡改進且怎麼改進?
模型選擇
名詞解釋(Vocabulary)
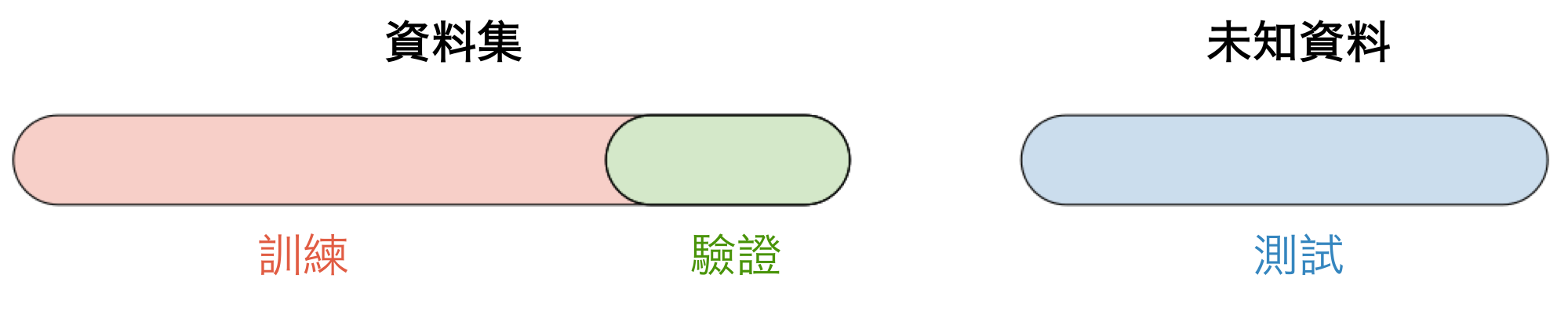
在選擇模型時,我們將數據分為的3個不同部分:
| 訓練集 | 驗證集 | 測試集 |
|---|---|---|
| 模型訓練 一般數據集中的80% | 模型評估 一般數據集中的20% 又叫保留集或開發集 | 模型預測 未知數據 |
一旦選擇了模型,就會在整個數據集上進行訓練,並在測試集上進行測試。如下圖所示:
交叉驗證(Cross-validation)
交叉驗證,簡稱 CV,是一種不必特別依賴於初始訓練集的模型選擇方法。下表匯總了幾種不同的方式:
| k-fold | Leave-p-out |
|---|---|
| 在 k-1 份上訓練,並在剩於的那份上評定,同常 k=5 or 10 | 在 n-p 份資料上訓練,並在剩於的 p 份上評定 當 p=1 時,稱作 leave-one-out |
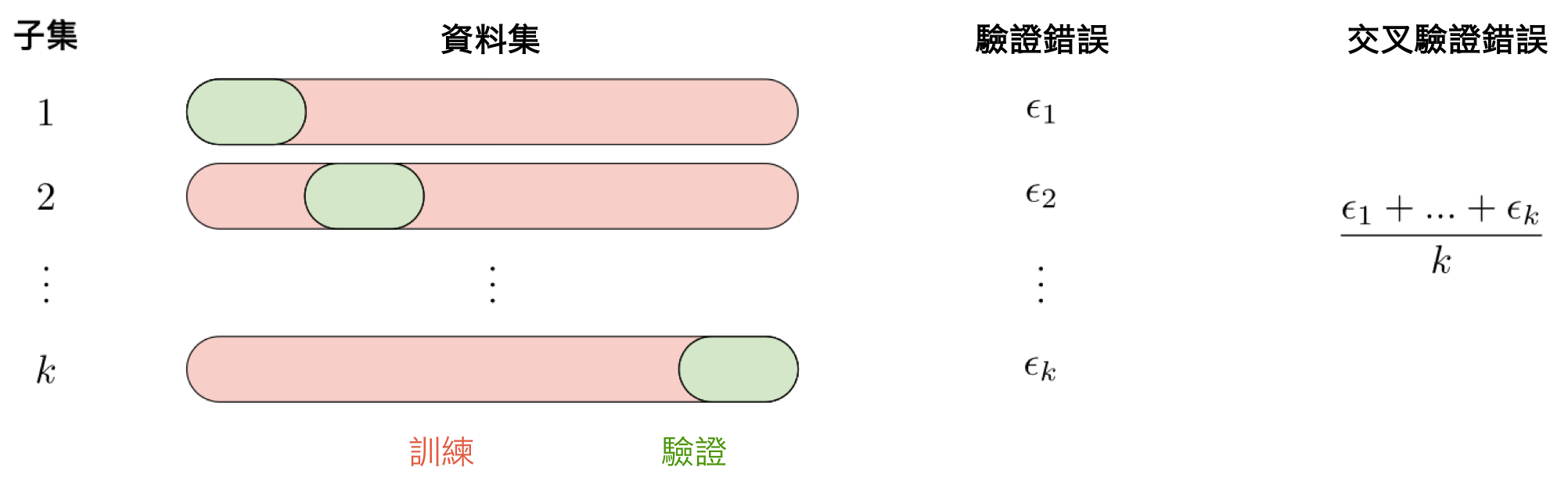
最常用的方法稱為 k 折疊交叉驗證,並將訓練數據分成 k 個折疊以在一個折疊上驗證模型,同時在 k-1 個其他折疊上訓練模型,所有這些 k 次。 然後將誤差在 k 倍上平均,並命名為交叉驗證錯誤。
正則化(Regularization)
正則化過程目的在於避免模型過度擬合訓練資料,從而處理高方差問題(high variance issues)。 下表總結了不同類型的常用正則化技術:
| LASSO | Ridge | Elastic Net |
|---|---|---|
| 將係數縮小為 0 有利於變量選擇 | 使係數更小 | 在變量選擇和小係數之間進行權衡 |
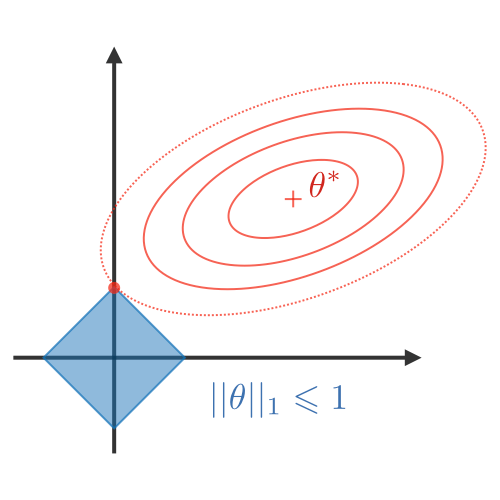 | 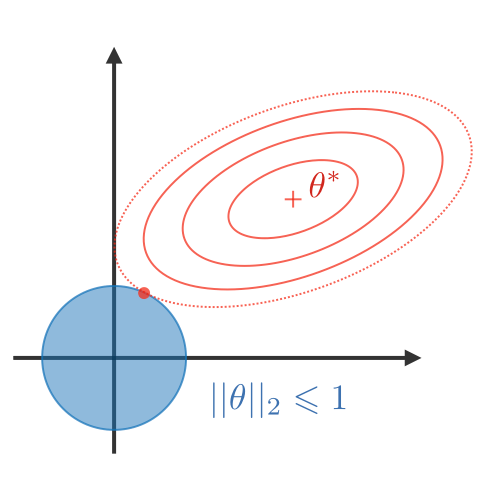 | 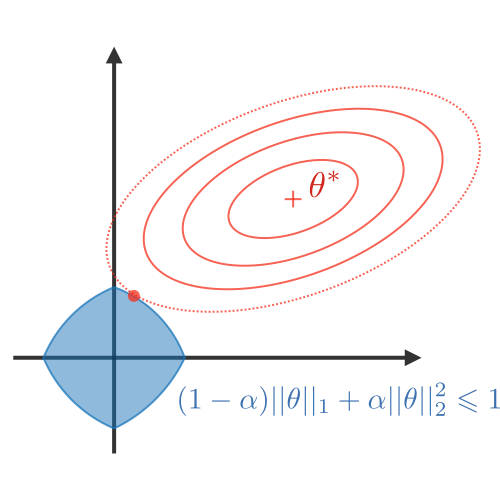 |
| $\lambda||\theta||_1\lambda\in\mathbb{R}$ | $\lambda||\theta||_2^2\lambda\in\mathbb{R}$ | $\lambda\Big[(1-\alpha)||\theta||_1+\alpha||\theta||_2^2\Big]$ $\lambda\in\mathbb{R},\alpha\in[0,1]$ |
分類指標
在處理二元分類問題時,以下為一些常見的評估指標。
混沌矩陣(Confusion matrix)
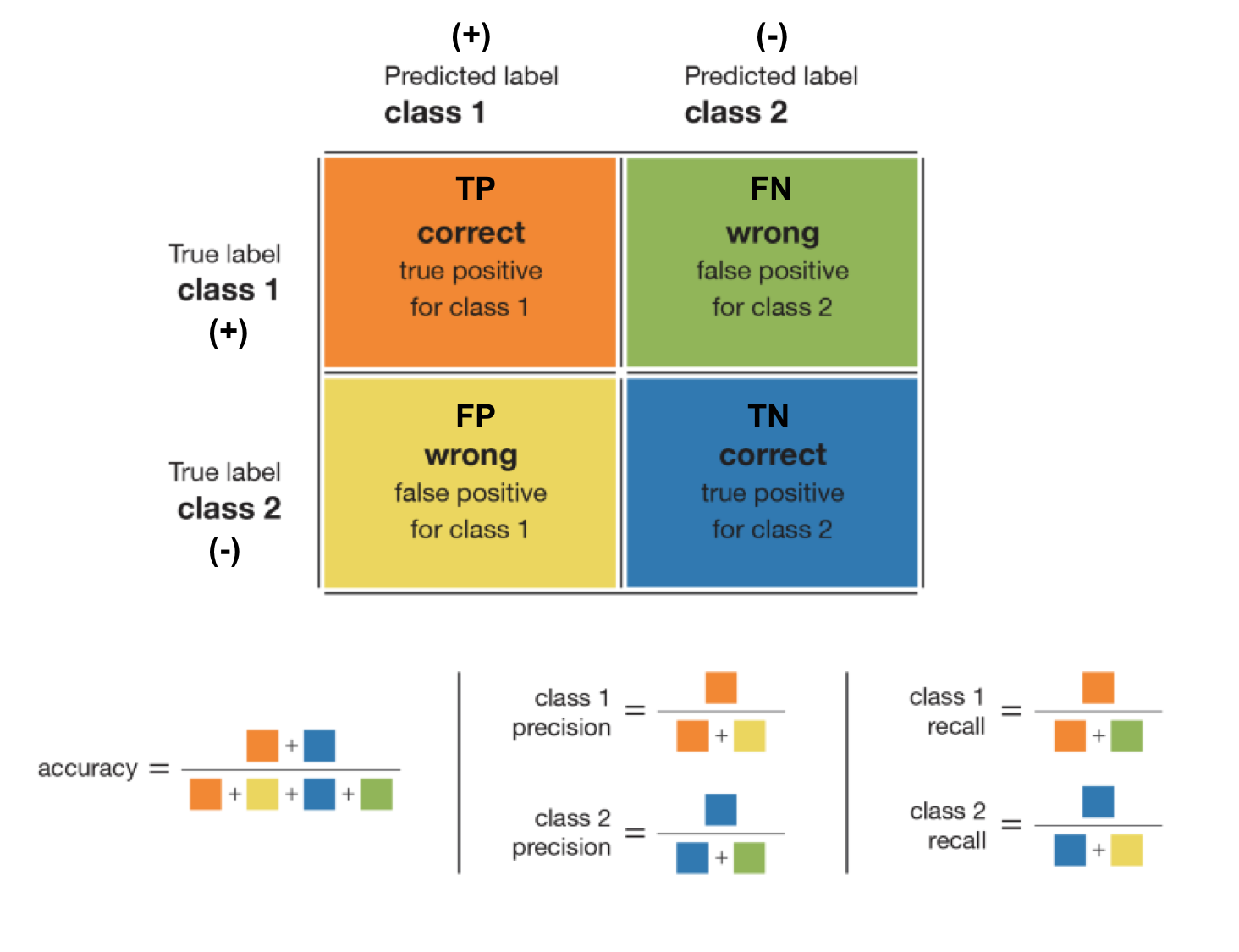
主要測量指標
| 性能指標 | 公式 | 說明 |
|---|---|---|
| 準確率(accuracy) | $\displaystyle\frac{\textrm{TP}+\textrm{TN}}{\textrm{TP}+\textrm{TN}+\textrm{FP}+\textrm{FN}}$ | 正確預測的數量除以預測總數。 |
| 類別精度(precision) | $\displaystyle\frac{\textrm{TP}}{\textrm{TP}+\textrm{FP}}$ | 以 Positive 為例,表示當模型判斷一個點屬於該類的情況下,判斷結果的可信程度。 |
| 類別召回率(recall) | $\displaystyle\frac{\textrm{TP}}{\textrm{TP}+\textrm{FN}}$ | 以 Positive 為例,表示模型能夠檢測到該類的比率。 |
| F1 分數 (F1 score) | $\displaystyle\frac{2 \textrm{TP}}{2 \textrm{TP}+\textrm{FP}+\textrm{FN}}$ | 以 Positive 為例,混合度量,對於不平衡類別非常有效。 |
對於一個給定類,精度和召回率的不同組合如下:
- 高精度+高召回率:模型能夠很好地檢測該類。
- 高精度+低召回率:模型不能很好地檢測該類,但是在它檢測到這個類時,判斷結果是高度可信的。
- 低精度+高召回率:模型能夠很好地檢測該類,但檢測結果中也包含其他類的點。
- 低精度+低召回率:模型不能很好地檢測該類。
ROC
受試者工作曲線,又叫做 ROC 曲線,它使用真正例率 (True Positive Rate) 作為縱軸和假正例率 (False Positive Rate ) 作為橫軸並且進過調整閾值繪製出來。下表匯總了這些度量標準:
| 性能指標 | 公式 | 等價形式 |
|---|---|---|
| True Positive Rate (TPR) | $\displaystyle\frac{\textrm{TP}}{\textrm{TP}+\textrm{FN}}$ | Recall, sensitivity |
| False Positive Rate (FPR) | $\displaystyle\frac{\textrm{FP}}{\textrm{TN}+\textrm{FP}}$ | 1-specificity |

有效性不同的模型的 ROC 曲線圖示。左側模型必須犧牲很多精度才能獲得高召回率;右側模型非常有效,可以在保持高精度的同時達到高召回率。
AUC
AUROC(Area Under the ROC),即ROC曲線下面積。可以看出,AUROC 在最佳情況下將趨近於1.0(近於0.0也是辨識能力佳的模型,但須將曲線反向),而在最壞情況下降趨向於0.5。同樣,一個好的 AUROC 分數意味著我們評估的模型並沒有為獲得某個類(通常是少數類)的高召回率而犧牲很多精度。
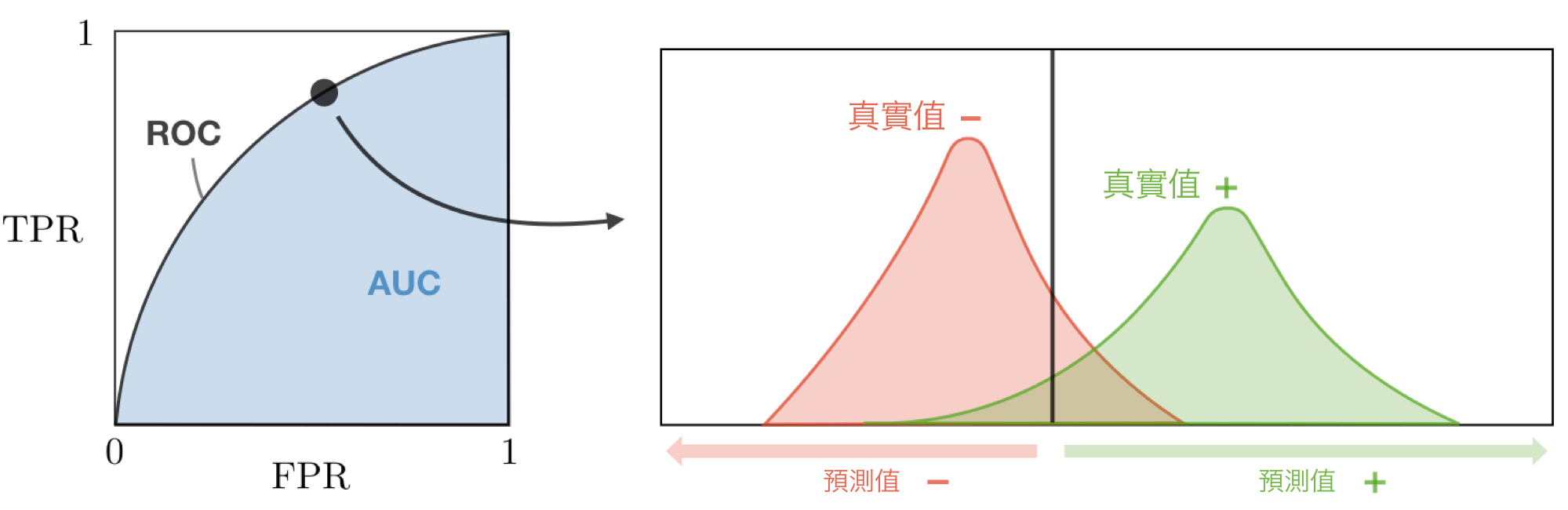
回歸指標
基本性能指標
給定一個回歸模型 $f$ ,下面的度量標准通常用來評估模型的性能。
| 性能指標 | 公式 | 說明 |
|---|---|---|
| 均方根誤差(RMSE) | 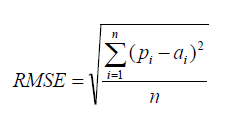 | RMSE 是衡量回歸模型錯誤率的常用公式。但是它只能在以相同單位測量誤差的模型之間進行比較。 |
| 相對平方誤差(RSE) | 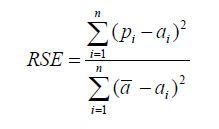 | 與 RMSE 不同,可以在不同單位測量誤差的模型之間比較相對平方誤差(RSE)。 |
| 平均絕對誤差(MAE) | 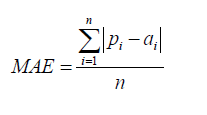 | 平均絕對誤差(MAE)與原始數據具有相同的單位,並且只能在以相同單位測量誤差的模型之間進行比較。它的大小通常與RMSE相似,但略小。 |
| 相對絕對誤差(RAE) | 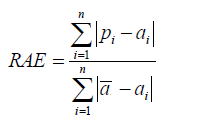 | 與 RSE 一樣,可以在不同單位測量誤差的模型之間比較相對絕對誤差(RAE)。 |
a = actual target, p = predicted target
確定性係數
確定性係數,記作 $R^2$ 或 $r^2$,提供了模型複現觀測結果的能力,如果回歸模型是“完美的”,則 SSE 為零,並且 $R^2$ 為 1。如果回歸模型是完全失敗,則 SSE 等於 SST,沒有方差被回歸解釋,並且 $R^2$ 為零。相關公式定義如下:
$\boxed{R^2=\frac{\textrm{SSR}}{\textrm{SST}}=1-\frac{\textrm{SSE}}{\textrm{SST}}}$
| 性能指標 | 公式 |
|---|---|
| 總平方和 (Sum of Squares Total) | $\displaystyle\textrm{SST}=\sum_{i=1}^m(y_i-\overline{y})^2$ |
| 迴歸平方和 (Sum of Squares Regression) | $\displaystyle\textrm{SSR}=\sum_{i=1}^m(f(x_i)-\overline{y})^2$ |
| 平方誤差和 (Sum of Squares Error) | $\displaystyle\textrm{SSE}=\sum_{i=1}^m(y_i-f(x_i))^2$ |
主要性能度量
以下性能度量通過考慮變量 n 的數量,常用於評估回歸模型的性能:
| Mallow’s CP | AIC | BIC | Adjusted $R^2$ |
|---|---|---|---|
| $\displaystyle\frac{\textrm{SSR}+2(n+1)\widehat{\sigma}^2}{m}$ | $\displaystyle2\Big[(n+2)-\log(L)\Big]$ | $\displaystyle\log(m)(n+2)-2\log(L)$ | $\displaystyle1-\frac{(1-R^2)(m-1)}{m-n-1}$ |
$L$ 代表近似,$\widehat \sigma^2$ 代表方差估計。
診斷與改善
偏差(Bias)
模型的偏差(Bias)指的是根據訓練資料學習出的模型在輸出預測結果時與真實樣本的差距。
方差(Variance)
模型的方差(Variance)指的是根據訓練資料學習出的模型在輸出預測結果時的變異程度(類別數)。
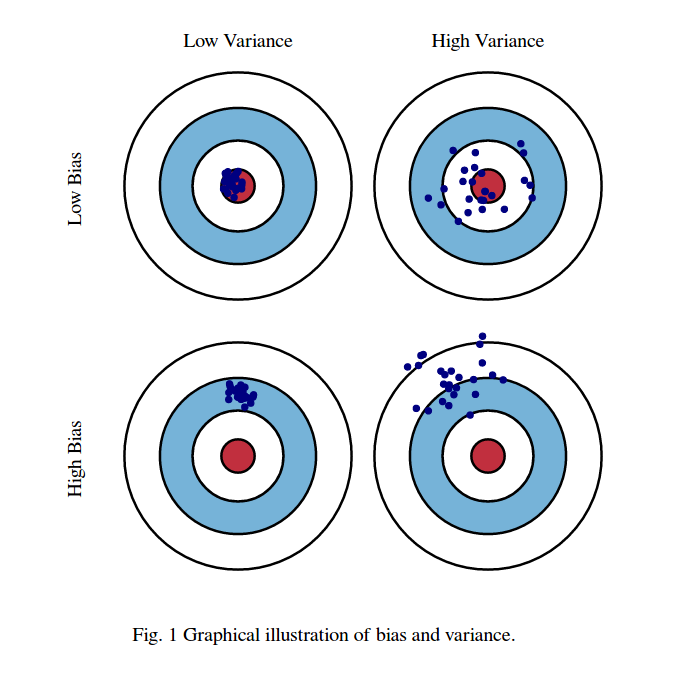
一個分類動物圖片的 model 來說明上圖的四種狀況,說明如下:
- Low Bias & Low Variance: 我們丟入一百張狗的圖片,model 預測的結果都是狗這個類別,即靶心處。
- Low Bias & High Variance: 我們丟入一百張狗的圖片,model 預測的結果有貓有狗但結果都分佈在這兩個類別。
- High Bias & Low Variance: 我們丟入一百張狗的圖片,model 預測的結果都是貓這個類別,即藍圈處。
- High Bias & High Variance: 我們丟入一百張狗的圖片,model 預測的結果有貓有鳥等其他類別,但因 Bias 所以沒有我們預期的結果狗。
偏差/方差權衡(Bias/Variance tradeoff)
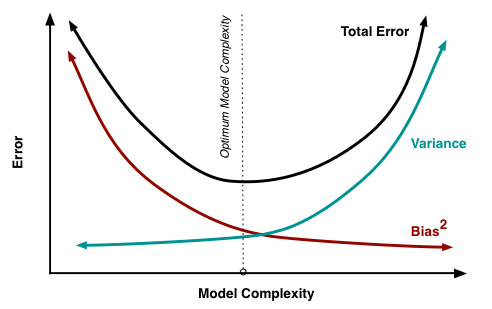
如上圖,如果我們的模型太簡單並且參數很少,那麼它可能具有 High Bias 和 Low Variance。另一方面,如果我們的模型具有大量參數,那麼它將具有 High Variance 和 Low Variance。因此,我們需要找到正確/良好的平衡,而不會過度擬合(overfitting)或欠擬合(underfitting)數據。
| Underfitting | Just Right | Overfitting | |
|---|---|---|---|
| 症狀 | • 高訓練誤差 • 訓練誤差接近測試誤差 • 高偏差 | • 訓練誤差略低於測試誤差 | • 極低訓練誤差 • 訓練誤差遠低於測試誤差 • 高方差 |
| 回歸圖例 | 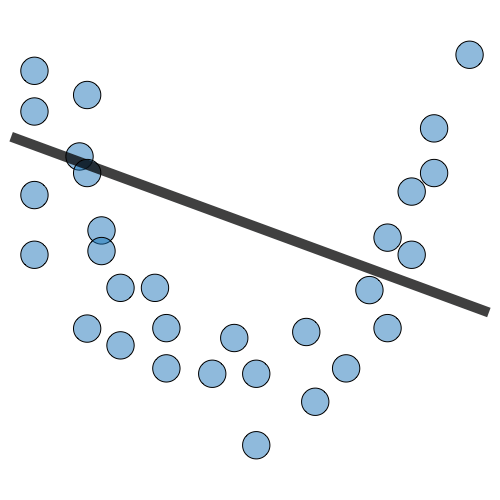 | 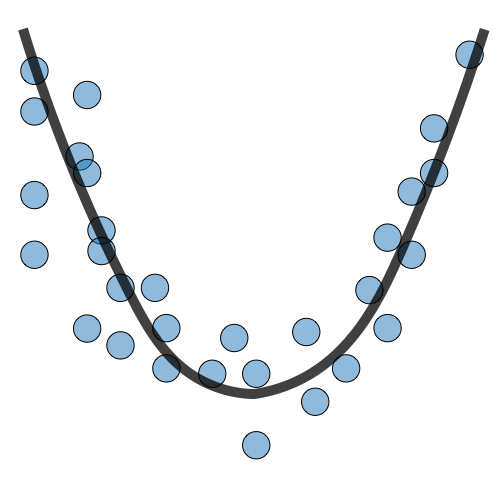 | 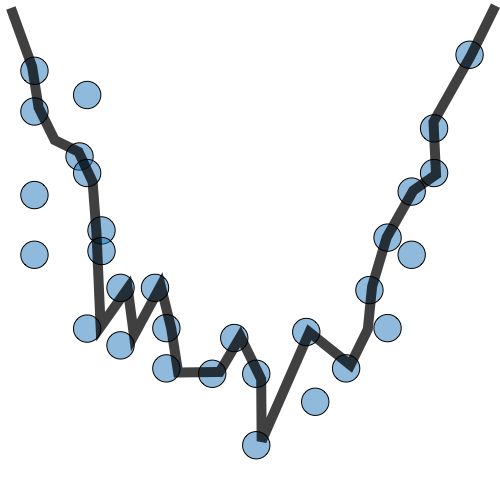 |
| 分類圖例 | 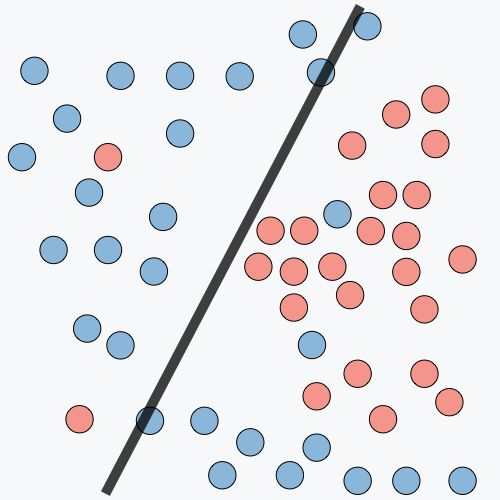 | 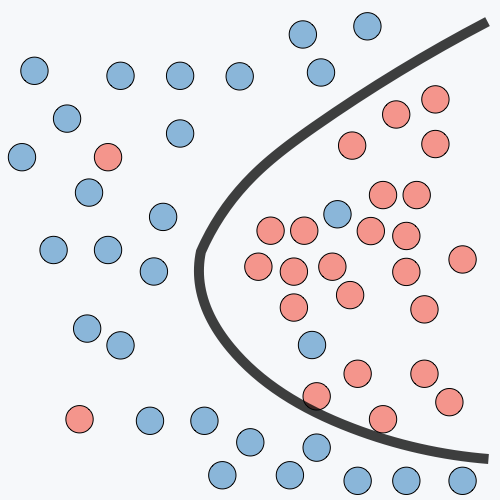 | 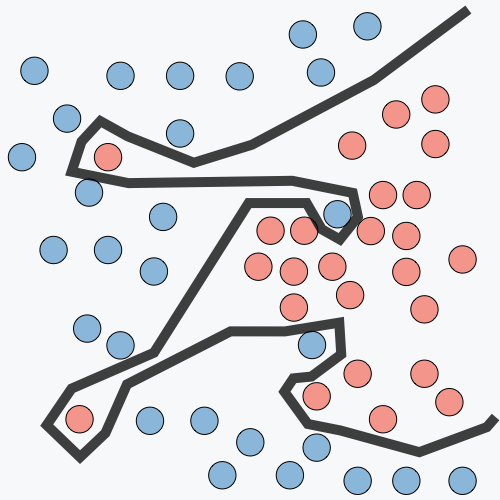 |
| 深度學習圖例 | 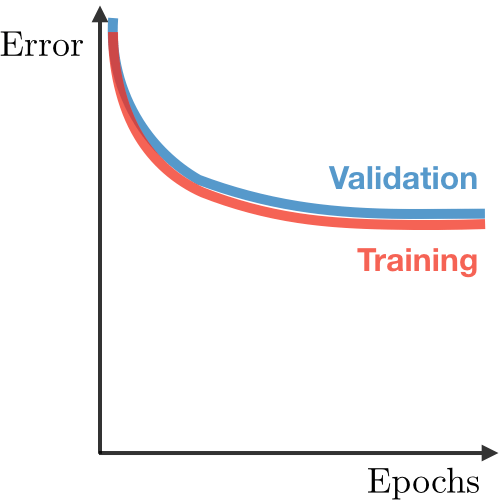 | 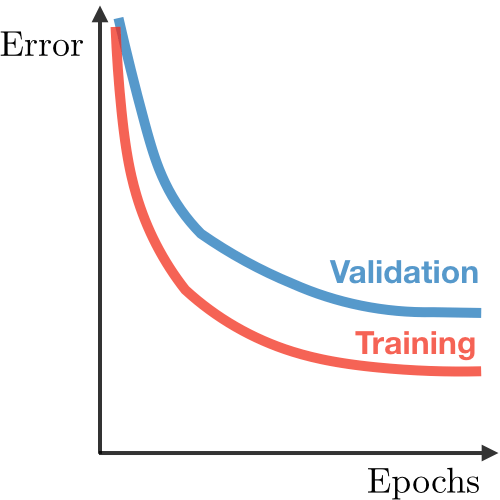 | 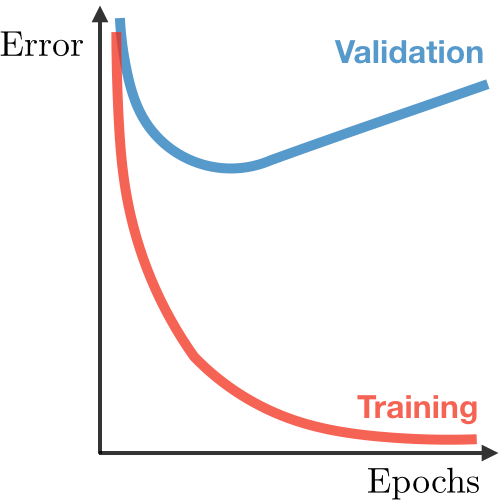 |
| 補救措施 | • 模型複雜性 • 添加更多特徵 • 訓練更長時間 | • 實施正則化 • 獲得更多數據 |
參考資料
comments powered by Disqus